Hepimiz günlük hayatımızda farkında olmadan hipotezler kuruyoruz ve karar vermeye çalışıyoruz onu mu yapsam bunu mu yapsam diye. Örneğin çocuğum 3 yaşına geldi kreşe mi versem , yoksa bir süre daha evde anneannesiyle birlikte kalmaya devam mı etse, yada İstanbul da yaşam masrafları epey arttı acaba daha küçük nüfuslu, ekonomik olarak daha rahat yaşayabileceğimi düşündüğüm memleketim olan Aydın’a geri mi dönsem gibi……. Peki bunları düşünürken ne yapıyoruz, düşündüğümüz seçenekleri tek tek tartıyoruz kafamızda, bir diğer deyişle test ediyoruz ve hali hazırda olan yaptığımız davranıştan vazgeçmek için , diğer seçeneğin bizim için daha mantıklı olduğuna ikna olmamız gerekiyor. Eğer ikna olamazsak hali hazırda olan davranışımızı yapmaya devam ediyoruz. İşte tüm bunları istatistiğe dayandırmadan yapıyoruz. Hadi o zaman şimdi istatistiksel olarak hipotez testlerinin mantığını anlayalım ve sık
kullanabileceğinizi düşündüğümüz bir kaç hipotez testini birlikte inceleyelim.
Hipotez Testi Nedir?
Geçerliliği olasılık esaslarına göre araştırılabilen ve karar verebilmek için öne sürülen
varsayımlara istatistikte “hipotez” denir.
Örneklem dağılımlarından elde edilen istatistiklere bağlı olarak, örneklem dağılımının,
parametresi bilinen kitleye ait olup olmadığı araştırılır. Hipotezlerin örneklem
yardımıyla incelenmesine “hipotez testi” denir.
Araştırma bulgularını yorumlarken, araştırmacıların bu bulguların tesadüfen meydana
gelip gelmediğini değerlendirmeleri gerekir. Hipotez testi, bir araştırma çalışmasının
sonuçlarının bir popülasyon için geçerli olan belirli bir teoriyi destekleyip
desteklemediğine karar vermek için sistematik bir prosedürdür.
Hipotez testinin adımları ;
–Araştırma hipotezinizi sıfır hipotezi(Ho) ve alternatif hipotez (H1) olarak belirtin.
–Uygun bir istatistiksel test gerçekleştirin.
–Sıfır hipotezinizi reddetmeye veya reddetmeye karar verin.
–Bulgularınızı sonuçlar ve tartışma bölümünde sunun.
Spesifik ayrıntılar değişebilse de, bir hipotezi test ederken kullanacağınız prosedür her
zaman bu adımların bazı versiyonlarını izleyecektir..
Sıfır hipotezi (H0), istatistiksel testlere bağlı olarak farklı şekilde ifade edilebilir, ancak iki
veya daha fazla değişken arasında fark, ilişki veya bağımlılık olmadığı iddiası olarak
genelleştirilebilir. Yani hali hazırda yaptığımız davranız.(Örn: Şuan İstanbul’da yaşıyor
olmam)
Alternatif hipotez (H1), sıfır hipotezi ile çelişir ve ilişkilerin var olduğunu iddia eder. Doğru
olduğunu kanıtlamak istediğimiz hipotezdir. (Örn: Memleketim olan Aydın’a yerleşmek)
Bununla birlikte, her zaman sıfır hipotezinin doğru olduğunu varsaydığımız ve sıfır
hipotezini reddetmek için kanıt bulmaya çalıştığımız bir yaklaşım vardır istatistikte.
Güven Aralığı ve Anlamlılık Düzeyi
Bir kitle parametresinin belirli bir güven aralığında olmasının ihtimalini verir.

P-Value
Hesaplanan p değeri istatistiksel testlere göre değişir. İlk olarak, gözlemlenen numune
verilerinin ortalama ve standart sapmasına bağlı olarak, test istatistik değerini
türetebiliriz. Daha sonra sıfır hipotezinin dağılımı verildiğinde bu test istatistiklerini alma
olasılığını hesaplayarak, p-değerini bulacağız.
Asıl kararı veren istatistiksel önem değeri gibi düşünebilirsiniz. Çoğu durumda kendi
kendine hesaplaancak ve biz tüm kararı p-value değerine göre vereceğiz.
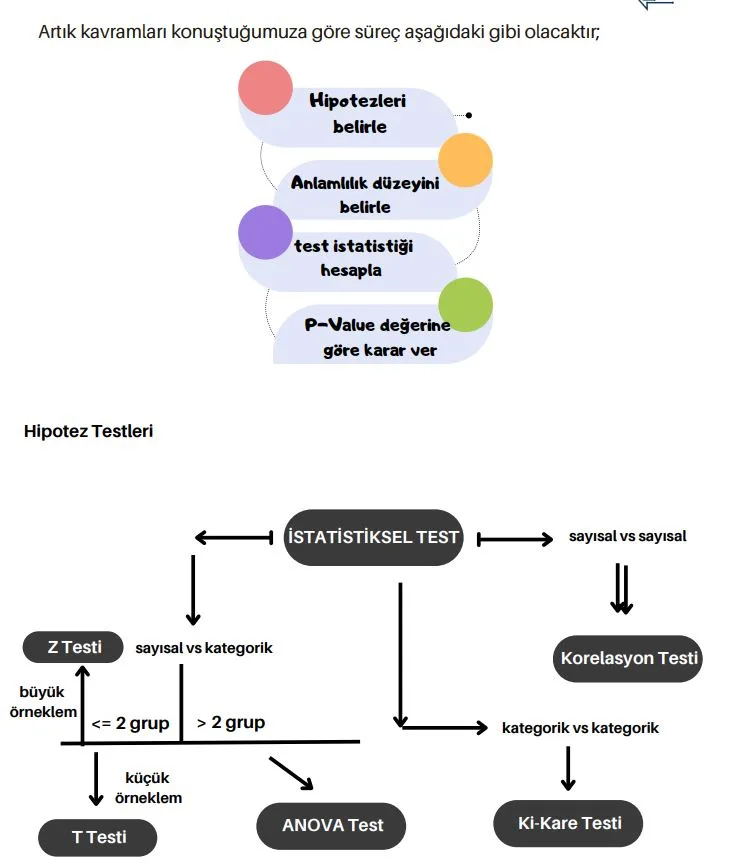
T-testi: Küçük örneklem büyüklüğüne sahip iki sayısal değişken grubunu/kategorisini
karşılaştırır.
Z-testi: Büyük örneklem büyüklüğüne sahip iki sayısal değişken grubunu/kategorisini
karşılaştırır.
ANOVA testi: Sayısal değişkenlerin iki veya daha fazla grubu/kategorisi arasındaki farkı
karşılaştırır.
Ki-Kare testi: İki kategorik değişken arasındaki ilişkiyi inceler.
Korelasyon testi: İki sayısal değişken arasındaki ilişkiyi inceler.,
Hipotez Testi Örneği
Kullandığım veri seti “Müşteri Kişilik Analizi” bu çalışmada farklı istatistiksel test türlerini
Python ile birlikte göstereceğiz.
T-testi, ANOVA ve Ki-Kare testi. Büyük örneklem büyüklüğüne duyarlıdırlar ve örneklem
büyüklüğü büyük olduğunda neredeyse kesinlikle çok küçük p-değeri üreteceklerdir.
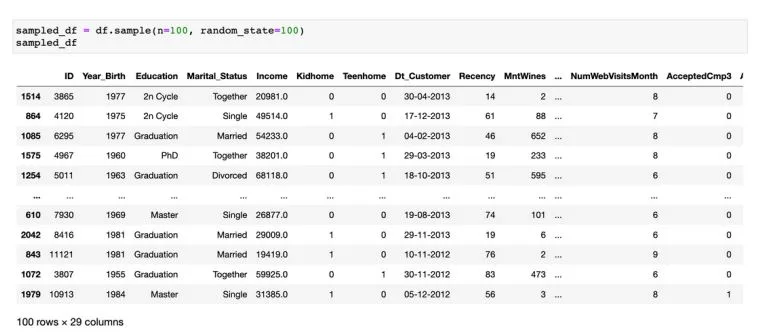
Bu nedenle, orijinal verilerden rastgele bir örnek (100 satır büyüklüğünde) aldım:
T-Testi
Sayısal bir değişken ile kategorik bir değişken arasındaki ilişkiyi test etmek
istediğimizde t-testi kullanılır.
T-testinin üç ana türü vardır.
Tek örneklem t-testi: bir grubun ortalamasını sabit bir değere karşı test eder.
İki örnek t-testi: iki grup arasındaki ortalama farkını test eder.
Eşleştirilmiş örneklem t-testi: aynı deneğin iki ölçümü arasındaki ortalama
farkını test eder.
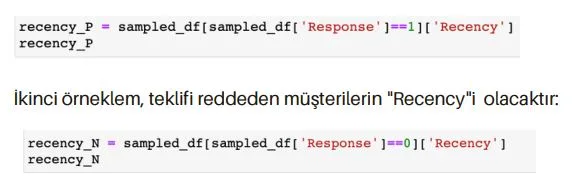
Örneğin, “Recency”in (müşterinin son alışverişinden bu yana geçen gün sayısı)
“Response” (müşterinin son kampanyadaki teklifi kabul edip etmediği) tahminine
katkıda bulunup bulunmadığını test etmek istersem, iki örneklem t testi
kullanabilirim.
İlk örneklem, teklifi kabul eden müşterilerin “Recency” i olacaktır:
1.Adım: Sıfır ve alternatif hipotezi tanımlayın.
H0 (Sıfır Hipotez): Son kampanyada teklifi kabul eden müşteriler ile teklifi kabul
etmeyen müşteriler arasında Receny açısından fark yoktur.
H1(Alternatif Hipotez): Teklifi kabul eden müşterilerin Recency oranı, teklifi kabul
etmeyen müşterilere kıyasla daha düşüktür.
2.adım : Uygun testi seçin.
İki bağımsız örnek arasındaki farkı test etmek için iki örnekli t-testi en uygun
istatistiksel testtir. Sıfır hipotezi doğru olduğunda test istatistikleri, öğrenci t-dağılımını
takip eder. t dağılımının şekli, iki örneklem boyutunun toplamı eksi 2 olarak
hesaplanan serbestlik derecesi ile belirlenir.
Python kitaplığı scipy.stats ile aşağıdaki gibi t dağılımını oluşturun

3.adım: P-değerini hesaplayın.
ttest_ind(), tüm bunları bizim için otomatik olarak yapan, Python’da bağımsız t-testi
için kullanışlı bir işlevdir. Parametre olarak iki örnek rececency_P ve recency_N
seçelim.
alternatif = ” less” seçin ve t-istatistiklerini ve p-değerini elde ederiz.
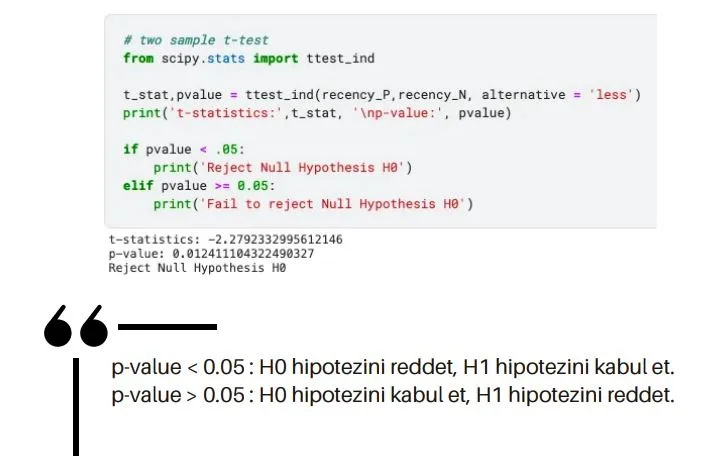
4.adım: Test sonucunu yorumlayın
Yaygın olarak kullanılan anlamlılık düzeyi eşiği 0,05’tir.
Buradaki p değeri (0.012) 0.05’ten küçük olduğu için toplanan örneğe göre
istatistiksel olarak anlamlı olduğunu söyleyebiliriz.
Teklifi kabul eden müşterinin daha düşük bir recency değeri olması muhtemelen
tesadüfen oluşmaz.
ANOVA Testi
Artık bir veya iki örneklem grubunun ortalamasını karşılaştırmak için t-testinin
kullanıldığını biliyoruz. İkiden fazla numuneyi test etmek istersek ne olur? ANOVA
testini kullanılırız.
ANOVA, gruplar arasındaki varyansın bir grup içindeki varyansa oranını hesaplayarak
gruplar arasındaki farkı inceler. Daha büyük oran, gruplar arasındaki farkın rastgele
şanstan ziyade grup farkının bir sonucu olduğunu gösterir.


Ki-Kare Testi
Ki-Kare testi, iki kategorik değişken arasındaki ilişkiyi test etmek içindir. Altta yatan
ilke, eğer iki kategorik değişken bağımsızsa, o zaman bir kategorik değişken, diğer
kategorik değişken değiştiğinde benzer bir bileşime sahip olmalıdır. “Education” ve
“Response”un bağımsız olup olmadığı örneğine bakalım.
1.Adım: Sıfır ve alternatif hipotezi tanımlayın.
H0: “Education” ve “Response” birbirinden bağımsızdır.
H1: “Education” ve “Response” birbirine bağımlıdır.
2.adım : Uygun testi seçin.
2 kategorik veri arasında kıyaslama için istatistiksel test olarak ki-Kare testi seçilmiştir.
Ki dağılımı, (satır — 1) x (sütun — 1) olarak hesaplanan serbestlik derecesi ile
belirlenir.

3.adım: P-değerini hesaplayın
Değişkenleri Ki-Kare testinin gerçekleştirilebilmesi için statsmodel kütüphanesi
chi2_contingency kullanabiliriz.

4.adım: Test sonucunu yorumlayın.
Bu istatistiksel olarak anlamlı olmadığını düşündürür. Bu nedenle, bu iki kategorik
değişkenin bağımsız olduğu sıfır hipotezini reddedemeyiz. Birbirininden bağımsızdır.
Bu yazımızda , üç yaygın istatistiksel test uygulamalarını yaptık:
T-testi, ANOVA testi ve Ki-Kare testi.
Hipotez testindeki temel mantık hep aynıdır: